This section describes key concepts in research and statistical inference with special emphasis on assessing physical activity. The issues raised in this section are important regardless of the specific physical activity assessment protocol chosen. Key distinctions between the terms “measurement,” “assessment,” and “evaluation” are first explained, followed by principles of sampling and calibration that have specific implications for physical activity research. Specific attention will then be given to distinctions between reliability and validity so that viewers can effectively interpret tools summarized in the Measures Registry. Brief coverage of advanced concepts of measurement research concludes this section but detailed summaries are beyond the scope of the Guide.
The terms “measurement,” “assessment,” and “evaluation” have important distinctions that need to be considered in physical activity research. The three items are often used interchangeably; however, they have very distinct meanings and interpretations. Measurement involves collecting specific information about an object or event and it typically results in the assignment of a number to that observation. Assessment is a broader term that refers to an appraisal or judgment about a situation or a scenario. Physical activity cannot be directly measured in the same way that height or weight are measured (for example) so the term “assessment” is generally preferred when referring to efforts to quantify the type or amount of physical activity that is performed. Available “measures” are each used to assess physical activity with varying degrees of error and this must be considered when interpreting the information. Evaluation involves attributing a meaningful value to the information that is collected. As expected, evaluation denotes placing a “value” on the obtained measurement. The values can be compared to a reference population (i.e., are “norm-referenced”) or to some type of standard (i.e., are “criterion-referenced”). Note, with both measures, a value is placed on what the individual has achieved.
The key point is that the three words each have different meaning and cannot be used interchangeably. In the context of physical activity, the measure could be a set of responses obtained through a recall tool (e.g., the amount of time walking or playing tennis), the assessment refers to the procedures used to determine the estimate of time spent in physical activity, and the evaluation would determine whether the person met the established physical activity guidelines or not.
Another important distinction in measurement and evaluation is that of sample vs. population. It is certainly unrealistic to obtain information from every single member of a population, so a sample is typically used to reflect the population of interest. The distinction between sample and population is analogous to the inherent differences between a measure and an estimate. In essence, we are attempting to measure behaviors of a population with estimates obtained from a sample of individuals. We must infer and “speculate” what the estimate or sample would be equivalent to if we had a true measure from all of the individuals in the target population. This process is defined as inferential statistics and it consists of replication of the population parameters of unknown distributions by examining the distributions in a subset of individuals who were randomly selected and are part of the population of interest. Random sampling is a condition that is often not satisfied, so our inferences are typically based on convenience samples (i.e., individuals not randomly selected from a population). It is important that the sample drawn randomly represents the population to which one desires to generalize the results.
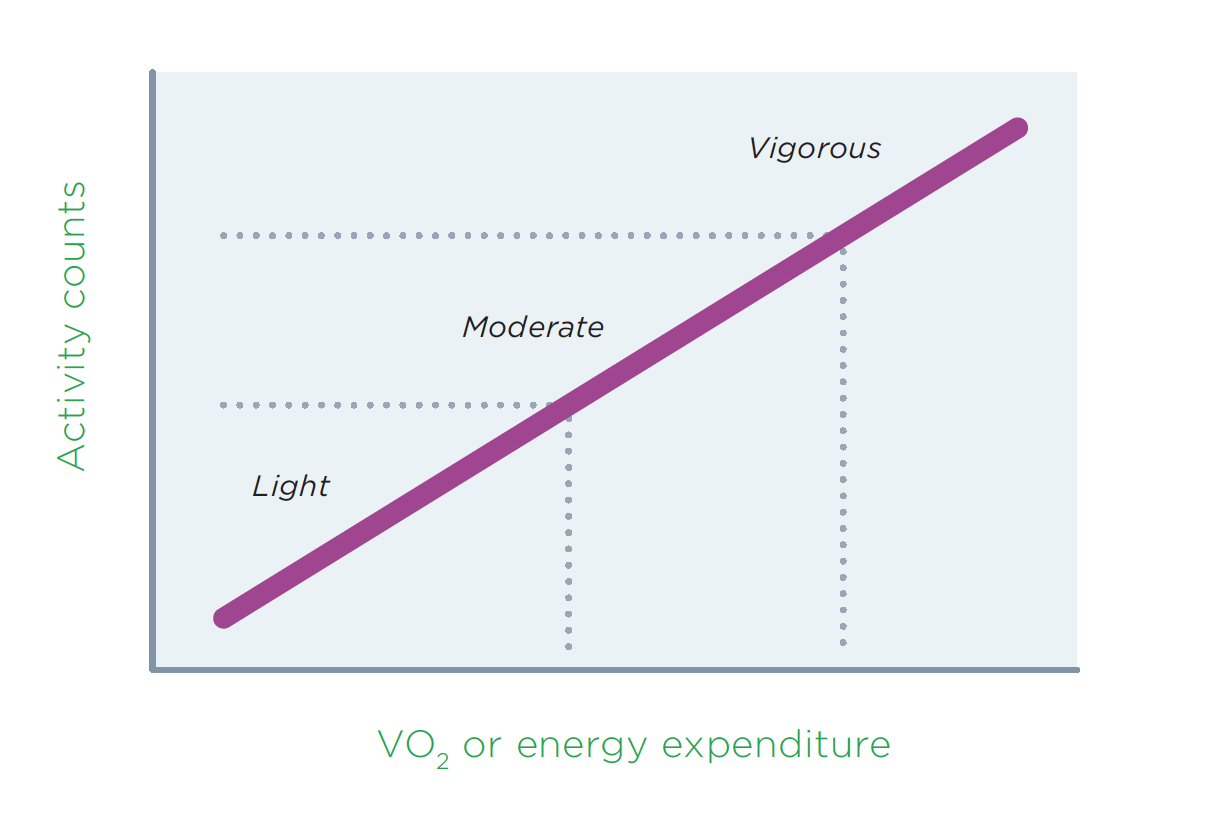
Another fundamental measurement consideration in physical activity research is that of calibration. As previously described, not all the dimensions of physical activity behavior can be directly measured, so assessment procedures typically necessitate a calibration process to obtain desired variables such as behavior type, VO 2 or energy expenditure. Monitor-based measures, for example, produce raw indicators of movement (e.g., activity counts) and these data must be translated to estimates of energy expenditure or other units to interpret the data (e.g., VO 2 or energy expenditure, minutes of MVPA). 35 The conceptual basis for calibrating activity monitors is depicted in Figure 4.
Figure 4: Conceptual Basis for Calibrating Activity Monitors

With a simple linear equation, algorithms could theoretically be developed to enable direct estimation of VO 2 or energy expenditure and categorization into LPA, MPA, or VPA. However, research has demonstrated that simple relationships are inadequate to capture the array of different activities performed under free-living conditions. 36 This is because the relationship between movement counts and energy expenditure varies greatly depending on the type of activity performed. The use of multiple equations or more complex pattern recognition approaches are now increasingly common for calibration purposes, but applying these methods requires additional expertise because the methods are not built directly into the software.
Some examples of more advanced methods will be introduced in later sections of this Guide (see Section 9) to facilitate additional exploration, but it is important to first have a basic understanding of the calibration process and associated statistics because these values are reported in papers highlighted in the Measures Registry. Common statistical indicators used to evaluate the resultant accuracy of calibrated physical activity measures include the test of mean differences (e.g., paired t-test), the Bland Altman procedure, and the Standard Error of Estimate (SEE). However, a detailed review of these terms is beyond the scope of the Guide.
Regardless of the instrument or method used to assess physical activity behaviors or movement, users are often (and must be) concerned with the reliability (consistency) and validity (truthfulness) of the obtained measures. The distinctions of these two indicators are described along with statistics used to express them.
Reliability refers to the consistency with which something is measured but it can be examined in several ways. For example, one might consider consistency of a response at a given point in time (e.g., How consistently does a person respond to the same question if it is administered on two occasions?). This would be analogous to having a person complete a physical activity questionnaire twice with a 30-minute interval in between. The comparison of the scores would reveal the extent to which the physical activity measure can provide similar and consistent information about activity levels. Reliability in this context is rarely assessed in physical activity assessment research because any short gap between two assessments will be confounded by memory. In other words, individuals are likely to remember what they answered and replicate their responses when asked to respond to the same questions. Alternatively, one can think of reliability across a longer period of time (e.g., How consistent are individual physical activity behaviors performed across a full week?) and avoid the short-term bias. This latter reliability, often referred to as stability reliability, provides information about the stability of the measure across a longer period of time. It is relatively easy to interpret the stability of a measure assessing a relatively stable (trait), characteristic but it is challenging to evaluate and interpret in the context of physical activity assessment. The assumption of stability reliability in measuring physical activity is confounded by changes in physical activity patterns that occur from day to day, morning vs. afternoon, and weekday vs. weekend. As described in Section 3, children and youth have very particular movement patterns and, therefore, any measure is highly susceptible to low stability reliability indices. This has considerable implications because a low index of stability reliability is more likely to reflect variability in behavior rather than the properties of the assessment tool. Thus, it can prove difficult to separate out the reliability of the assessment tool from the reliability of the behavior.
Reliability is evaluated using interclass comparisons (based on the Pearson Product Moment correlation) or intraclass comparisons (based on analysis of variance). Using the interclass reliability is somewhat restrictive because it is limited to two points in time and does not take into account changes across time. It is important to note that the interclass reliability coefficient can be perfect even if the measures being compared are constantly changing. For example, if all participants increase their self-reported physical activity by about 30 minutes a day, the stability reliability for a full week would be very high. However, this example does not actually show stability (i.e., consistency) in the behavior but instead shows a systematic change in physical activity levels across the measurement period. The intraclass method is more robust and can examine consistency across multiple measures or over multiple days. The intraclass (alpha coefficient) reliability permits a more accurate estimate of the reliability. The intraclass reliability coefficient also is used to estimate the internal consistency reliability of a questionnaire or survey. The internal consistency reliability does not mean that the instrument is necessary reliable (consistent) across time. Rather, it means that the items on the instrument generally tap the same construct (i.e., measure the same outcome). This type of reliability is also very popular in social sciences but may have limited utility in the context of physical activity assessment. Again, consider the example of a questionnaire that asks about activity in different contexts (e.g., recess, physical education, after-school). Activity levels at each of these settings will vary and it is possible that a child would report low levels of physical activity at recess and after-school but indicate high amounts of physical activity at physical education. These various scores across different contexts (and items) would result in low internal consistency and indicate that the items do not assess the same construct when, in fact, they do. Depending on the measure being tested, the general use of reliability in physical activity research is more useful to assess variability in physical activity behavior and not the ability of the specific measure to provide consistent scores. For example, the agreement between two observers when coding observed physical activity behavior would be an important test of inter-rater reliability for the observation method and would indicate consistency of scores across testers or coders. Regardless of the type of reliability coefficient calculated, the range of possible reliabilities is zero to 1.0, with higher values indicating greater consistency between the various measures. The Standard Error of Measurement (SEM) is often reported to reflect the degree to which a score might vary due to measurement error.
Validity refers to the truthfulness of the measure obtained. A measurement tool can result in reliable information but the data may not truthfully reflect the reported amount of physical activity behavior or movement. Validation of physical activity measures is typically accomplished with concurrent procedures in which a field or surrogate measure is compared with another more established or criterion measure. As shown in Figure 3, criterion measures are often used to calibrate monitor-based measures and these, in turn, are often used to calibrate report-based measures. From a validity perspective, the self-report physical activity measures are compared to this criterion to provide evidence of the truthfulness of the reported physical activity behaviors. These issues are discussed in Section 5. The Standard Error of Estimate (SEE) is often reported to reflect the degree to which an estimated value might vary due to measurement error.
Reading and interpreting the reliability and validity results in research reports can be difficult. Authors often make little reference to their procedures (other than to say, “the results were reliable” or “the measure has been validated”). Therefore, it is important to carefully review the procedures used to support reliability or validity of a specific measurement tool or process. The Measures Registry provides brief summaries of reliability and validity statistics but it is important to carefully review the actual study before determining whether it will have utility for a specific application. A number of different indicators are used to report reliability and validity; however, for the aforementioned reasons we will focus on the most popular indicators for validity. Table 1 provides a summary of common research statistics used to evaluate and report validity. Most would also be useful to determine reliability but the types of statistics will depend on whether the measures are continuous scores (e.g., steps per week) or categorical (e.g., achievement of physical activity guidelines).
Table 1: Summary of Validity Indices Used in Physical Activity Research
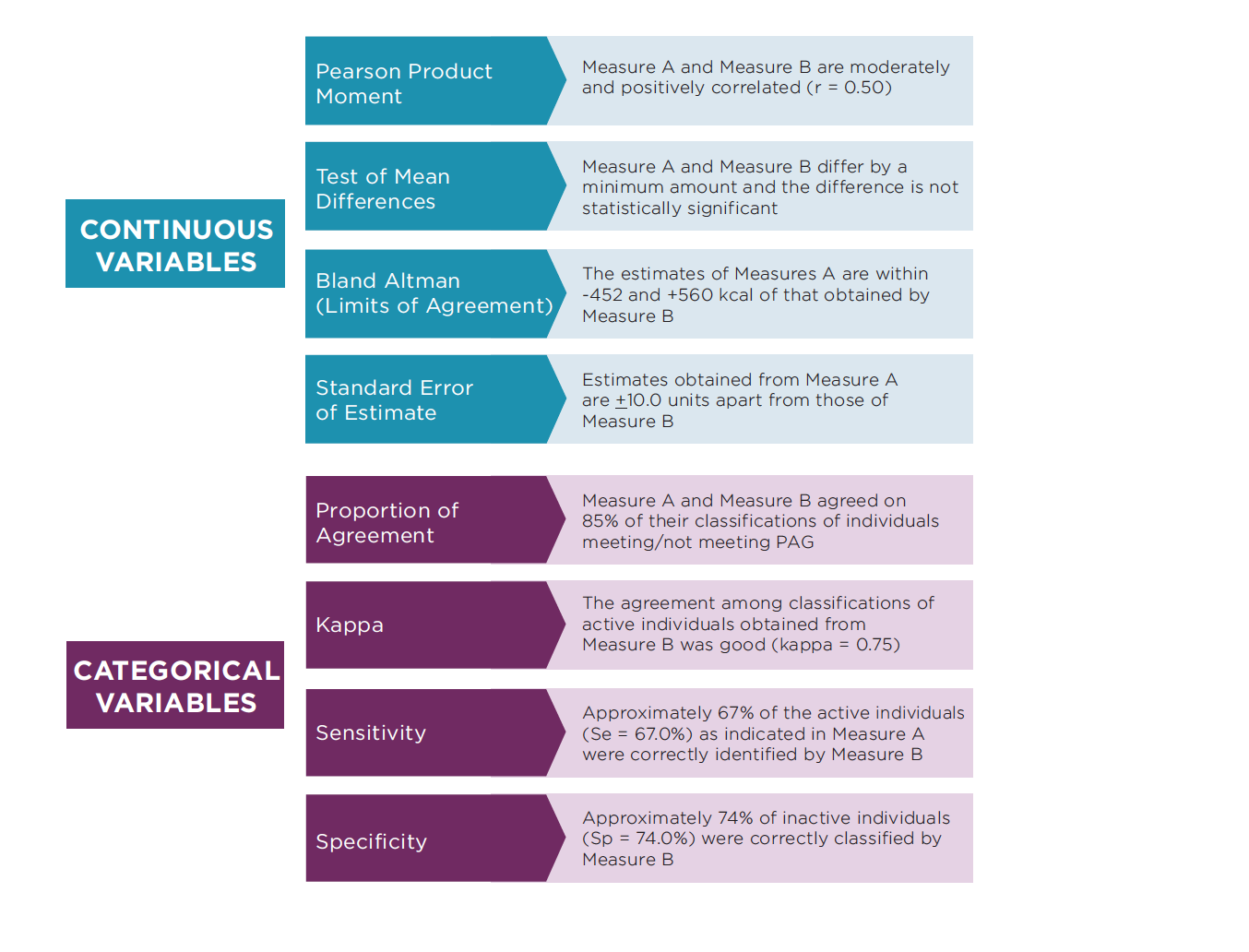
When evaluating research findings on different physical activity methods, it is important to carefully consider the actual strength of the associations and not simply the statistical significance. Research studies tend to focus on “statistical significance” to determine whether a value is reliable or valid, but significance is directly influenced by a number of factors, including sample size. To avoid over-interpreting findings, it is important to evaluate the absolute agreement and outcome measures rather than just the statistical significance. For example, focus should be on the magnitude of a Pearson Correlation Coefficient rather than the significance. Traditional interpretations characterize correlations below 0.4 as being low, 0.4 to 0.8 as moderate, and above 0.80 as being high. Validity indices of most report-based measures are below 0.4 (i.e., low), while values for monitor-based measures are at the high end of this scale (i.e., 0.6 to 0.8 or higher).
With validity statistics it is also important to keep in mind that the reported relationships are typically based on aggregated data from multiple people. This makes sense from a sampling perspective, but accurate group-level estimates of physical activity do not necessarily translate to accuracy for estimating individual physical activity levels. A useful indicator that captures the error for individual estimation is the Mean Absolute Percent Error (MAPE). As the name implies, the MAPE value reflects the mean absolute difference in outcomes and is computed by first calculating the absolute value of individual difference scores and then averaging them. This provides a more appropriate (and conservative) indicator of actual error for individual estimation because it captures the magnitude of both overestimation and underestimation. Studies that report mean error do not capture the actual amount of error because overestimation and underestimation may average out.
Consider a very simple example of two children who have energy expenditure levels estimated with both a physical activity questionnaire (PAQ) and the doubly-labeled water (DLW) method. Assume that Child 1 had a DLW estimate of 2600 kcal/day and a PAQ estimate of 1100 kcal/day and that Child 2 had corresponding values of 900 kcal/day for DLW and 2000 kcal/day based on the PAQ. The average value from these two individuals is 1750 kcal/day for DLW and 1550 kcal/day for the PAQ. The group difference in the estimates is only 200 kcal/day (approximately 11 percent error) and may not be statistically significant. However, the group means mask the large individual error of 1500 kcal/day for Child 1 (i.e., underestimation) and 1100 kcal/day for Child 2 (i.e., overestimation). The absolute error for the individual estimates are 58 percent for Child 1 and 122 percent for Child 2 (leading to a computed mean value or MAPE of 90 percent).
Group means are typically evaluated in traditional validation studies, but it is important to not assume that this level of error would hold for individual estimates, as the example illustrates. A method may be reported to provide “valid” estimates for group-level comparisons, but error can be considerably higher when attempting to estimate values for individuals. Measures also can differ greatly at the individual level, yet it is possible (and common) for the measures to be moderately correlated (e.g., r = 0.40) and for group differences to be relatively small. Understanding the difference between individual- and group-level estimates is key to this distinction. d
A final point about interpreting validity statistics is to understand that significant associations do not imply equivalence or agreement. The scenario introduced above is further expanded to illustrate this. Envision that the estimates obtained from the DLW method are compared with two different physical activity questionnaires (PAQ 1 and PAQ 2) and that PAQ 2 provides estimates of energy expenditure that are twice as high as those obtained from PAQ 1 (see Table 2, which is adapted from Zaki et al. 37 ). The average daily estimates of energy expenditure for DLW, PAQ 1, and PAQ 2 are 1712.8 kcal, 1733.5 kcal, and 3467 kcal, respectively. The PAQ 1 and PAQ 2 estimates are both strongly correlated with DLW (r = 0.88), perhaps indicating similar “agreement.” However, the estimates from PAQ 1 differ from the DLW method by 20.7 kcal (at the group level) while estimates from PAQ 2 differ by 1754.2 kcal. The PAQ 2 assessment substantially overestimates energy expenditure even though it is highly correlated (r = 0.88) with the outcome measure. This example illustrates the limited value of correlations because it shows the inability to infer the presence or absence of systematic differences between two estimates. Measures that are correlated may be sufficient if the goal is to simply distinguish the most active individuals from the least active. However, in other situations, it may be important to be able to estimate the actual amount of physical activity performed or the overall energy expenditure. Therefore, care must be used when interpreting outcomes validity statistics from studies summarized in the Measures Registry or in other publications.
Table 2: Example of Agreement in Estimates of Energy Expenditure (kcal/day) Using the Pearson Correlation
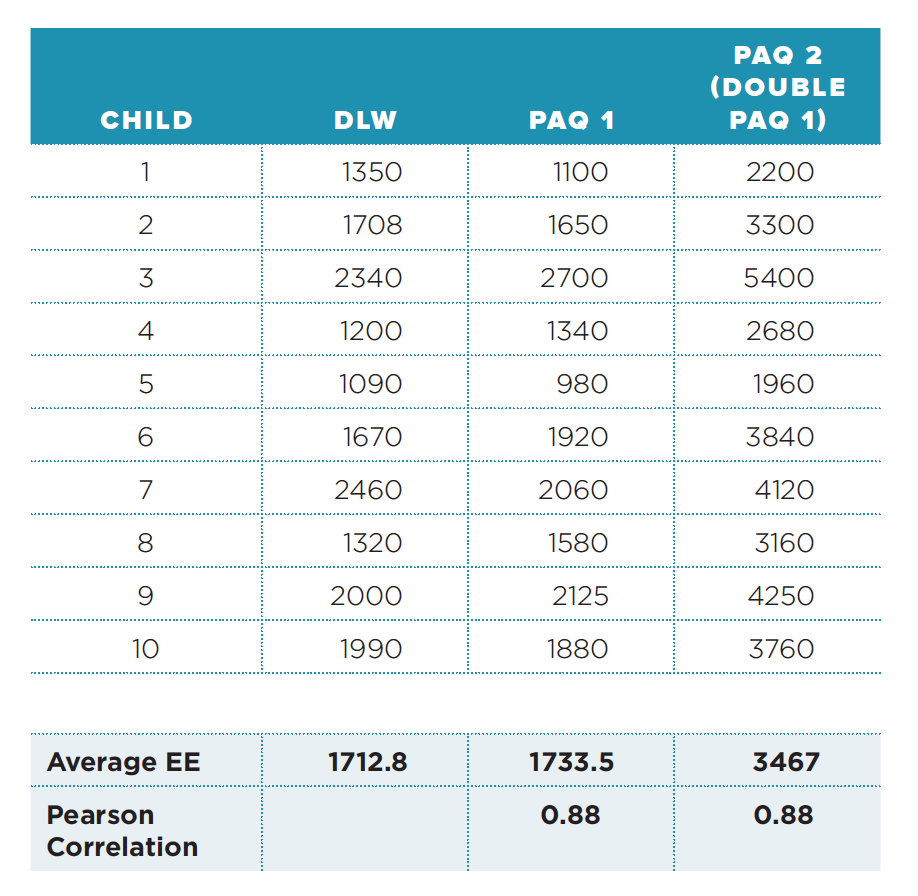
Source: Zaki et al.
Regardless of reliability and validity, it is important to remember that data collected from all measurement tools are estimations of the behavior or movement. Measurement errors cannot be avoided, but researchers must distinguish between systematic and random errors as well as the sources of error in research and evaluation. In considering effects of error, researchers should consider the relative importance of obtaining estimates of individual behavior or whether group level estimates are sufficient. As previously illustrated, data reported at the individual level will generally have more error than aggregate summary values that reflect the means of a sample of individuals. In many situations, group-level estimates are all that are needed, but it is important to minimize and control sources of error when possible.
A key challenge in research is to minimize not only error in the measure itself (i.e., closely related to validity as described above), but to control for error in the measurement procedure. Overall, error can be attributed to multiple sources and divided into specification error, measurement error, and processing error.
Specification error occurs when the measurement method does not match the actual concept being studied. This is hard to avoid in physical activity research because the specific “construct” investigators are trying to capture often cannot be directly observed. For example, researchers are frequently interested in evaluating “typical” or “habitual” physical activity, but existing methods may capture only a few isolated days or a week and therefore do not directly capture the construct.
Measurement error refers to error that arises in obtaining a response or a measure during data collection. This occurs in research because physical activity is inherently difficult to assess and because our methods have important limitations. Examples include limitations of technology in capturing movement, mistakes in recording data, respondent errors in reporting or recalling data, and deliberate or subconscious bias in the reported data. Measurement error is generally assumed to be more of a problem in report-based measures due to their inherent subjectivity. However, equally challenging forms of measurement error complicate assessments with various monitor-based methods.
Processing error must be considered when manipulating raw data to produce outcome or summary variables. It occurs because it requires the researcher to summarize, aggregate, and categorize the data, and these steps necessitate a number of assumptions. Examples include assigning METs to process data or using algorithms or prediction equations to convert movement data into outcomes.
Being cognizant of the types of errors can help in designing more effective studies and in appropriately interpreting outcomes.
Statistical power refers to the concept of identifying relationships between variables when such relationships truly exist. The essence of inferential statistics is to investigate the relationship between variables. Statistical power is a key concern in intervention studies where the goal may be to determine whether a particular program or treatment increased MVPA in children. The ability to detect an association (i.e., have statistical power) depends on a number of factors, but the accuracy (i.e., validity) of the measurement instrument is one of the most important. With inaccurate measures it is possible for a researcher to incorrectly conclude that there is no relationship between the intervention and the intended outcome simply because the MVPA outcome is not accurately assessed. For example, think of an outcome (e.g., cardiovascular disease) and an exposure variable (e.g., participation in physical activity) that are moderately correlated. The sample size required to find this association with a 95 percent statistical power might increase by two- or three-fold depending on the accuracy of the measure selected to assess physical activity. This illustrates how the accuracy of the measure can have important implications for study design by affecting statistical power. Technically, the lack of accuracy of a measure and inability to detect a true association is referred to as an error of the second type (i.e., a Type II error). A Type II error can be made for a variety of reasons but a main one is a lack of a reliable measure that reduces the statistical power to identify a relationship. A detailed description of the interaction between statistical power and validity is beyond the scope of this Guide, but researchers and practitioners should be aware that error, as defined based on the previous descriptions, of validity reduces power and makes it difficult to detect associations when they actually exist.
A common need in measurement research is to evaluate the equivalence of different measures. This is important for all calibration applications discussed previously and is typically expressed as a measure of group-level agreement. In many cases, a more practical field-based measure is evaluated to determine whether it agrees with a more expensive and accurate lab-based measure. For example, monitor-based instruments are often calibrated to estimate energy expenditure, so it is important to evaluate whether the procedure can produce group-level estimates that are statistically equivalent to a criterion measure obtained from indirect calorimetry or DLW. Measurement researchers often evaluate agreement between measures with the graphical Bland Altman method 37-38 but this method does not provide a way to empirically (or statistically) evaluate agreement. Standard statistical tests (e.g., ANOVAs or t-tests) are often used to compare measures but these are designed to test differences and are fundamentally flawed for evaluating agreement. Because the significance is influenced by sample size, studies with larger and more robust samples are more likely to detect significant differences than studies with fewer participants, regardless of the size of the difference. This issue relates to the concept of statistical power described above and has led many studies to erroneously conclude that two measures are equivalent when a non-significant difference is detected (or that two measures are not equivalent when a difference is significant). This is analogous to an intervention effect that is likely to be significant if the sample being assessed is considerably larger (i.e., great degree of statistical power). Therefore, working with larger groups is often desirable. In the context of physical activity assessment, a large sample will have the opposite effect and improve the likelihood to detect small differences between two measures even though these might not be relevant (i.e., not meaningful; not clinically important). This would artificially minimize the chances that the measure being tested is not deemed similar to the criterion assessment of physical activity. Alternative methods of “equivalence testing” avoid the inherent limitations of traditional statistical tests of differences and are more appropriate for evaluating agreement, e,39 This approach has not been widely adopted so it is possible for studies to erroneously conclude that measures agree or that they are valid. The main message is that it is important to understand the limitations of traditional statistical methods when evaluating agreement between alternative measures.
d Obtaining precise estimates of individual physical activity and energy expenditure is extremely challenging and is an unrealistic goal for most eld-based measures. Therefore, it is important to recognize the limitations of the estimates, particularly when extrapolating or reporting estimates at the individual level. Parallel progress is being made with reducing error in monitor-based measures and developing and refining measurement error models for report-based measures.
e According to classic hypothesis testing for differences, the null hypothesis is that the differences between the two measures are not equal to “0” (i.e., differences are “non-random”). This is a rather unrealistic scenario, as no measure will result in identical values when compared to another. Equivalence testing ips the null hypothesis and this enables zones of equivalence to be established a priori and to be tested statistically. Details about equivalence testing methods are beyond the scope of this Guide, but the main point is to understand that equivalence testing is a more appropriate way to examine agreement than are standard tests of differences. Considering this issue when reviewing instruments and outcomes can help to facilitate interpretations.